The following pages provide a quick overview into DMRG.x, a distributed-memory implementation of the DMRG algorithm based on the PETSc and SLEPc libraries.
Source code: https://github.com/jnvance/DMRG.x
Documentation: https://dmrgx.readthedocs.io
Tutorial Resources: https://github.com/jnvance/DMRGTutorial
Abstract
The Density Matrix Renormalization Group (DMRG) algorithm is a numerical technique used in the study of low-dimensional strongly correlated quantum systems. With this implementation, one can study two-dimensional spin systems using a one-dimensional traversal of the lattice.
In particular, the current version deals with a square-type lattice with longitudinal dimension \( L_x \) and transverse dimension \( L_y \) shown in the following figure. The spin sites can interact with their nearest neighbor (NN) and next-nearest neighbors (NNN), and different boundary conditions may be implemented on the two directions (such as the cylindrical boundary conditions illustrated below).
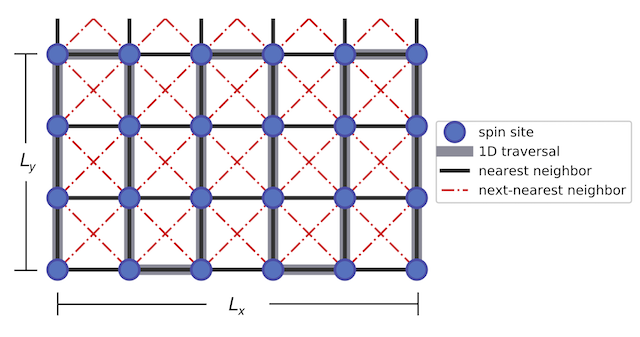
The Hamiltonian for this implementation takes the form:
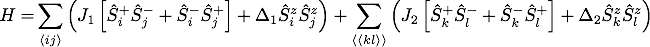
which maps to a Heisenberg model when \( J_1 = 1/2 \) and \( J_2 = \Delta_2 = 0 \), and to the J1-J2 XY model when \( \Delta_1 = \Delta_2 = 0 \).
To reduce the computational cost, we exploit \( U(1) \) symmetry through conservation of the total magnetization ( \( S_z \)). We also implement a matrix-free approach in the diagonalization of the superblock Hamiltonian.
Documentation
The full documentation generated with doxygen may be viewed in the link above. To generate the documentation yourself, go to the root directory and execute
$ make docs-default
which places the documentation in docs/default/html/index.html.
References
This application was developed as part of the following thesis for the Master in High Performance Computing Programme:
- J. Vance. "Large-Scale Implementation of the Density Matrix Renormalization Group Algorithm." (2017). [link]
For more information on the DMRG algorithm, we recommend the following reading materials:
- U. Schollwöck. "The density-matrix renormalization group." Rev. Mod. Phys. 77, 259 – Published 26 April 2005 [doi]
- A E Feiguin. "The Density Matrix Renormalization Group". In: Strongly Correlated Systems. Berlin, Heidelberg: Springer Berlin Heidelberg, Apr. 2013, pp. 31–65. [link]
To learn DMRG through a simpler implementation, we suggest starting from the following Python code:
- James R. Garrison, & Ryan V. Mishmash. (2017, November 29). simple-dmrg/simple-dmrg: Simple DMRG 1.0 (Version v1.0.0). Zenodo. [link]
Credits
Author:
This application was developed in collaboration with the Condensed Matter and Statistical Physics Section of the The Abdus Salam International Centre for Theoretical Physics, under the supervision of:
License
MIT License. Copyright (c) 2018 James Vance.
See full text of LICENSE (view on github).

